A Novel Application of Maglev Graphite for Attitude Control of CubeSats by Guilherme Reis
From The Space Library
University of Victoria, Victoria, BC, Canada November 2015
Guilherme Reis1 Instituto Superior Técnico, Universidade de Lisboa, Lisboa, Portugal
Cass Hussman2; Afzal Suleman3
1 Graduate student, guilherme.horta.reis@gmail.com
2 Graduate student, hussmann@uvic.ca
3 Professor and Canada Research Chair, Department of Mechanical Engineering, suleman@uvic.ca
Contents |
Abstract
Attitude control and determination system of small satellites must be fast and accurate for applications such as camera pointing for earth or celestial observation or communication using precision pointing of an antenna. Current attitude control systems required fuel and a considerable amount of power, and can sometimes be hindered by mechanical systems failure. Here, a novel attitude control system is proposed using the diamagnetic characteristics of magnetic levitating pyrolytic graphite in the Earth’s magnetic field. Diamagnetic materials can self-levitate when subjected to a static magnetic field. Furthermore, the diamagnetic properties of pyrolytic graphite depend on temperature. Using this characteristic, it is possible for the graphite to generate a torque by simply heating small sections of it. On this paper, this phenomenon is studied and analyzed and its applications are discussed. In particular, the ECOSat cubesat, currently being developed by the University of Victoria, will carry a payload experiment specifically designed to explore and validate this phenomena in space. One of the experiments will be composed of a plate of pyrolytic graphite that, under the influence of the Earth’s magnetic field, will produce a torque when a small section of it is heated using a semiconductor infrared LASER. With several of this small LASERs, several points of the graphite can be irradiated thus creating a torque along the required direction. The exposure time can be used to influence the maximum temperature change on the graphite plate and thus controlling the magnitude of the torque created.
Keywords: Optical control, attitude control, diamagnetism, pyrolytic graphite, magnetic actuator, LASER
1. Introduction
Diamagnetism is a property of a material that has been studied for a long time and is nowadays quite well understood. Bismuth and pyrolytic graphite are known as the most diamagnetic materials at room temperature. The Earnshaw Theorem does not allow stabilized levitation of a body only subjected to inverse-square law forces [1]. However, introducing diamagnetic materials of the levitation system enables a complete stabilization of the levitating body [2]. Furthermore, a magnetic field exerts a repulsive force on a diamagnetic material, enabling it to levitate on its own.
Unlike some other magnetic properties, diamagnetism is independent from the temperature of the material. Notwithstanding, it was discovered that the motion of a plate of pyrolytic graphite levitating on a magnet array could be optically controlled [3], this is evidence that, in the case of graphite, there must be some chance on the irradiated area to produce the forces that created this motion. Having in mind the possibility of creating a force on a pyrolytic graphite plate that is subjected to a magnetic field using simply a LASER, the ECOSat team, from the University of Victoria, idealized a system capable of creating a torque to control the attitude of a satellite. This system would use a few LASERs pointed near the borders of a pyrolytic graphite plate under the influence of the Earth’s magnetic field, in orbit. The unbalancing forces created during this act would create a torque that would be capable of controlling the satellite’s attitude.
2. Background
2.1. The Earth’s magnetic field
The dynamo effect describes how the motion of the fluid inside the Earth’s outer core can generate and maintain a magnetic field [4] strong enough to involve the entire planet. The pressure, gravitational and thermal gradients on the outer core dictate the laws by which the fluid is ruled and determine its movement. This movement of charges and ferromagnetic particles created the magnetic field that is surrounding the planet. As opposed to a simple dipolar magnet, the north and south poles of the Earth’s magnetic field are not aligned, neither with the center of the Earth neither with its rotational axis. Besides this irregularity, the field is not stationary: its intensity changes with time as well as the position of the poles on the planet’s surface. However, this changes are slow enough for it to still be used for orientation, attitude determination and navigation.
At the Earth’s surface, the magnetic field intensity ranges from 22 mT to 67 mT, being the most intense near the magnetic poles and the least intensive close to the magnetic aclinic line [5]. Then, with increasing altitude, the field’s magnitude decreases, for example: at 100 km height, the field’s intensity is 16 μT [6]. The field dependence with altitude, or distance to the center of the planet, cannot be described using simple mathematical formulations, ergo, usually Fourier models based of field spherical harmonics are used.
2.2. Diamagnetism
Whenever a material is subjected to a magnetic field, it will react to it on a certain way, characteristic of the material. Diamagnetism is the property on which the whole work of this dissertation stands on. All materials present a diamagnetic behavior, however, on the great majority of them this behavior is very weak and so it is negligible compared to the other forms of magnetism that the material presents. A diamagnetic material has a magnetic permeability lower than one, ergo, a magnetic material will repel any magnetic field that it is subjected to. Imposing the magnetic field to circle the material around as much as possible will create a repelling force between the diamagnet and the magnetic field. The diamagnetic properties of a material are usually characterized by a property called magnetic susceptibility, χ. The magnetic susceptibility is related to the magnetic permeability by the formula (1). A diamagnetic material has a magnetic susceptibility inferior to zero and with minimum value of -1.
The most diamagnetic material is pyrolytic graphite, with χV=-6.1e-4, [7], just followed by bismuth, with χV=-1.7e-4, [8]. Diamagnetic forces induced on materials from a magnetic field have a very different behavior from inverse-square law forces. While the attraction forces for other types of magnetism have an inverse quadratic relation with distance from the origin of the field, diamagnetic forced depend on the gradient of the squared magnetic field, as it is demonstrated on [9] and the final expression for the magnetic forces shown below:
In this expression, V is the volume of the diamagnetic material, μ0 is the vacuum magnetic permeability and B is the magnetic field. Although the diamagnetic behavior is weakly present of all material, there are some that have all other types of magnetism suppressed, so diamagnetism is the only observable interaction. Especially pyrolytic graphite and bismuth have the strongest diamagnetic behavior known (besides superconductors), this materials are used to stabilize magnetic levitation and can also levitate by themselves above an array of small Neodymium magnets or under the effect of a strong magnetic field.
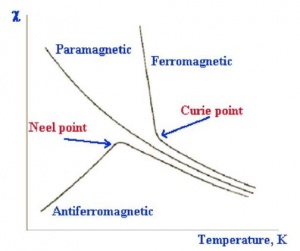
Figure 1: Variation on magnetic susceptibility of various types of magnetic materials with temperature [10].
2.3. Magnetic susceptibility, function of temperature
The effect of temperature on the magnetic behavior of materials is a phenomena that has been studied for a long time and is today well understood. Paramagnets and ferromagnets have their magnetic susceptibility decreased with increasing temperature, while antiferromagnets have their magnetic susceptibility increasing along with temperature, until the Neel Point is reached and then the magnetic susceptibility, χ, will drop with further temperature increased. These effects are shown on Figure 1.
Diamagnetism has never shown a variation with temperature and, besides the empirical evidence, it is mathematically understood this lack of dependence: as it is shown on the online page [11]. It is of general knowledge that diamagnetism is not affected by temperature, however, in the empirical research made by Kobayashi and Abe, it is shown that pyrolytic graphite has its magnetic susceptibility decreased when the temperature of the material is increased [12].
Figure 2: Variation on magnetic susceptibility of pyrolytic graphite with temperature [13].
Pyrolytic graphite is a very unique material, as it is the only known material which its magnetic susceptibility has a strong dependence with temperature. This behavior is shown on Figure 2. On the work by Kobayashi and Abe, the measurements on the variation of magnetic susceptibility were made along the measurement on the levitation height of a plate of graphite above an array of rare earth permanent magnets assembled in an antiparallel fashion. The plot on Figure 2 shows two lines: the blue one represents the decreasing (in absolute value) of the magnetic susceptibility of the graphite plate, as a consequence of this decrease in the diamagnetic behavior, the levitation height will decrease, as it is shown on the red line. It is noticeable that, for this range of temperatures, the magnetic susceptibility of the pyrolytic graphite plate has its dependence with temperature extremely close to a linear dependence.
3. Implementation
3.1. Experiment: Magnetic susceptibility change with temperature
The purpose of this experiment is to acquire data on the evolution of the magnetic susceptibility of graphite with varying temperature. It is now known that the magnetic susceptibility of pyrolytic graphite should decrease, in absolute value, with temperature in a nearly linear relation, as it was discussed before. Furthermore, also the levitation height will decrease with the increase of the temperature of the material. One of the goals of this experiment is to verify the data gathered by Kobayashi and Abe [14] and expand it for a wider temperature spectrum. With the data about this unique property of pyrolytic graphite, the understanding on how to create an acceleration or a torque on a plate of graphite subjected to a magnetic field will be highly enhanced. With a special regard to the lower temperatures found in a space environment, a broader temperature spectrum with relevant magnetic data is essential to develop the best design possible for an attitude control system using this technology. It is expected that the dependence from temperature of the magnetic susceptibility continues to present the nearly linear behavior even for much lower temperatures than the ones shown on Figure 2.
On this experiment, the data for the magnetization and magnetic susceptibility of a sample of pyrolytic graphite was gathered using a SQUID magnetometer. The pyrolytic graphite sample was subjected to a magnetic field of 1000 Oersted and the temperature of the sample was variated in the range of 2.1 °K to 300 °K.
3.2. Magnet array simulation
Figure 3: A CAD render of a plate of pyrolytic graphite levitating over a 10 by 10 array of neodymium magnets.
For a better comprehension of the physical phenomena that is on the basis of this dissertation, as well as an exercise to test the knowledge acquired during the research developed on its ambit, a MatLab® simulation was design and produced. On this simulation, the mechanics that rule the optical motion control of maglev graphite are explored, scrutinized and translated on a computational simulation. The temperature increase on the LASER irradiated area is computed, using the thermal and optical properties of pyrolytic graphite. Then, the deficit on magnetic susceptibility is calculated, using the trend-line obtained on the experiment, in order to make an analysis of the torque and acceleration that is applied on the plate by the local change in its magnetic properties. As the magnetic susceptibility of the irradiated area decreases, the levitation height will also decrease slightly and the plate will tilt in the direction of the irradiated area. This will create an unbalancing force that will propel the plate in that direction.
With a real assembly like the one depicted on Figure 3, it is possible, using a LASER, control the motion of the levitating plate over the array of magnets, as it was done on the paper by Kobayashi and Abe, [15]. When the LASER is focused near the border of the plate, it will quickly move on that direction. Focusing it on the center of the plate has no apparent effect. The simulation returns the horizontal components of the acceleration of the plate, the resulting levitation height and the tilt angles on the plate on the two horizontal angles.
3.3. Attitude control system
3.3.1. System design
The attitude control system designed and which physical concepts of operation were thoroughly studied and analyzed on the ambit of this project can be explained on a simple way. The main components of this actuator are: the various LASERs, the pyrolytic graphite plate, the satellite and, as the source of the diamagnetic force that the system exploits, the Earth’s magnetic field. The LASER will be turned on in order to rise the temperature of the section of the PG that it is focused on, close to the border, for maximum torque. This temperature rise will cause a decrease on the PG magnetic susceptibility, in absolute terms. This will result on a lower magnitude of the diamagnetic force that the Earth’s magnetic field is subjecting on the plate, for that irradiated section. As there is a force deficit on only one of the sides of the plate, this will result on a torque that will spin the satellite. With various LASERs, pointing at different spots on the plate, the irradiated spot’s location can be determined, enabling the creation of any torque required. By controlling the frequency at which the LASER is turned on, the temperature can be controlled, providing the chance to control the magnitude of the torque created.
Figure 4 shows a model of the system. The pyrolytic graphite plate is represented by the square, shown in perspective, the LASER beam is represented as the red column on the right and the effect of the Earth’s magnetic field is represented on the figure as the gradient of its square value. This mathematical entity is directed in the direction of decreasing intensity of the field, in this case (although not being important to this explanation) it points away from the Earth, almost radially. The magnetic field is actuating on the plate according to the law described by equation (2). When the section under the LASER beam is heated by it, and has its magnetic susceptibility decreased, in absolute value, there will be an unbalance of the force created by that section relative to its analogous, symmetric relatively to the center of the plate. This force deficit is shown on Figure 4 as dFm. This difference of forces between two symmetrical sections on the plate will create a torque, M, on the plate. By controlling the irradiated section of the plate, the direction of the torque can be controlled, furthermore, controlling the exposure time, the intensity of the torque can be also controlled.
Figure 4: Simple model of the attitude control system and ECOSat scientific payload that is being developed on the...
3.3.2. Orbital simulation
The main objective of this dissertation is to design an attitude control system resorting to the optical control of maglev graphite. As such, the first, and most important, computer simulation will be based precisely on this system. The simulation is developed using the MatLab platform. The model of the Earth’s magnetic field is based on the CHAOS-5 model using a compatible MatLab version which can compute the three components of the magnetic field for a given position.
The simulation will compute the torque, on and Earth Centered Inertial spherical coordinate system, that the system induces on the satellite by having one of the LASERs powered.
The Technical University of Denmark has developed several models for the Earth’s magnetic field using data from various satellites. The first CHAOS model of the magnetic field was accurate up to the fiftieth harmonic degree, for the static field, and up to the eighteenth for the first time derivative [16]. In 2014 the DTU publishes the CHAOS-5 model for the Earth’s magnetic field. The great importance of the data recovered by ESA’s three SWARM satellites is of utter importance for this model [17]. The data for this model was selected and treated with several criteria used previously for the older versions of the model. Emphasizing some of this criteria: only night-side data from geomagnetically quiet times, suitable for use in the CHAOS modelling scheme; geomagnetic activity at non-polar latitudes was sufficiently low; merging electric field at the magnetopause was sufficiently small for data from polar regions. The DTU provided a version of the model compatible with MatLab. This version was used along with the simulation every time that the three components of the magnetic field for a given position were needed.
Similarly to the magnet array simulation, using the same algorithm, this simulation begins by computing the temperature on the irradiated section and its modified magnetic susceptibility. Then the gradient of the squared magnetic field is computed for the orbital position the satellite is, as well as the force it creates on the plate. The force deficit and torque are then computed. This simulation takes into account the attitude of the satellite, ergo, the orientation of the plate relative to the magnetic field.
4. Results
4.1. Magnetic susceptibility change with temperature
The data gathered during this experiment is very extensive, a total of 490 measurements were made. These are shown on the plot in Figure 5. The plot shows very clearly the evolution of magnetic susceptibility of the pyrolytic graphite sample with the temperature. The equation shown on the plot corresponds to a trend line that, as it can be seen, has a close correlation with the data. A polynomial curve of seventh order was chosen as it was the lowest order to give a value of R squared of 1. This equation is used on the simulations to compute the magnetic susceptibility of the plate at the temperature reached with the LASER beam. As the temperature on the simulations will not rise much above 300 K, the same curve will be used for temperatures outside the measured spectrum.
It is obvious that, contrarily to what is generally thought about diamagnetism, the magnetic susceptibility of pyrolytic graphite depends on temperature.
Figure 5: Variation of the magnetic susceptibility (volume) of the sample of pyrolytic graphite measured by the SQUID magnetometer.
4.2. Magnet array simulation
The results of this simulation show values similar to what can be observed with an assembly like the one depicted on Figure 3. According to the simulation, the values of the final temperature and corresponding magnetic susceptibility of the irradiated section are: T = 395.92 °K χV = 1.5404e-06
Furthermore, the plot showing the convergence for the value of levitation height computed can be seen on Figure 6.
Figure 6: Variation of the levitating height with iteration step
It is noticeable the quick convergence on the beginning of the process and then a slower phase. This is due to the convergence of the tilt angles and consequent cancellation of the torque on the plate. When the torque on the plate is zero, the final height is then reached.
Finally, the acceleration created by the LASER on the plate are:
ax=0.1659 m/s
ay=0.1712 m/s
These values were the outputs of a simulation on which the LASER was pointed with a vector (0.02, 0.02) cm from the center of the plate. The different values of the acceleration computed are due to the difference in length and width of the plate, not being perfectly square.
4.3. Other applications
Magnetic levitation (maglev) is a highly advanced technology. It is used in the various cases, including clean energy (small and huge wind turbines: at home, office, industry, etc.), building facilities, transportation systems (magnetically levitated train, Personal Rapid Transit (PRT), etc.), weapon, nuclear engineering, civil engineering, advertising and so on. The common point in all these applications is the lack of contact and thus no wear and friction. This increases efficiency, reduce maintenance costs and increase the useful life of the system. The magnetic levitation technology can be used as a highly advanced and efficient technology in the various industrial. There are already many countries that are attracted to maglev systems [18]. One of the most common applications of maglev, and one of increasing demand and development, are maglev trains. These trains have the important advantage of not being supported by contact force, therefore, there is no energy loss due to the friction between the wheels and the train track. Maglev suspension systems are divided into two groups of electromagnetic suspension (EMS) and electrodynamic suspension (EDS). Another method to achieve levitation of a maglev train is proposed, Diamagnetic Suspension. This method of levitation would use electromagnets on the track, just like electromagnetic suspension, however, the train would have a base covered by pyrolytic graphite. Some calculations were computed to evaluate the viability of this method of suspension. Several approximations were made, which grand these calculation only an estimative value.
Using current technology electromagnetic tracks, and considering a 17,000 kg train, it would require a plate of graphite underneath it covering all its base. This plate would require a thickness of 8.3 mm. A train with this description would levitate at 2.5 cm from the track with a maximum velocity of 395 km/h.
5. Conclusions
In conclusion, it is certain that, contrarily to the general idea that diamagnetism is not dependent on temperature, the magnetic susceptibility of pyrolytic graphite certainly is. This means that the force generated by the magnetic field of Earth on the plate can be controlled using temperature variations on the plate. Having distinct sections of the plate at different temperatures, it shall be possible to generate a torque to influence the attitude of the satellite, which is the fundamental principle of this novel technology. It is crucial to further study this characteristic of pyrolytic graphite and explore its applications and unique properties. As an application as an attitude control actuator for a satellite, this system shows great potential, waiting to be estimated with the finalization of the orbital simulation. This will enable an estimation of the maximum torque that the system could create in orbit and contribute to greatly improve its design.
Acknowledgements
The author would like to thank the orientation given by Professor Afzal Suleman and by the opportunity to develop this project and be involved in the ECOSat team of the University of Victoria; Cass Hussman, team leader of the ECOSat project; Professor Natia Frank for the indispensable help with some of the experiments on the magnetic properties of pyrolytic graphite; and Professor Fernando Lau for the co¬orientation given to this project.
References
- ^ S. Earnshaw. On the Nature of the Molecular Forces which Regulate the Constitution of the Luminiferous Ether. Cambridge Philosophical Society, 1842.
- ^ M. D. Simon and A. K. Geim. Diamagnetic Levitation: Flying frogs and floating magnets. Journal of Applied Physics, 2000.
- ^ M. Kobayashi and J. Abe. Optical Motion Control of Maglev Graphite. American Chemical Society, 2012
- ^ D. P. Stern. The Great Magnet, the Earth. 2008. http://www.phy6.org/earthmag/dynamos2.htm
- ^ S. Maus, S. Macmillan, S. McLean, B. Hamilton, A. Thomson, M. Nair, and C. Rollins. The US/UK World Magnetic Model for 2010-2015. NOAA Technical Report NESDIS/NGDC, 2010.
- ^ C. C. Finlay, N. Olsen and L. Toeffner-Clausen. The CHAOS-5 Geomagnetic Field Model. 2015. http://www.spacecenter.dk/files/magneti c-models/CHAOS-5/
- ^ S. Davis. Investigation of Ceramic Pyrolytic Graphite and Applications. University of Victoria – Department of Mechanical Engineering, 2014.
- ^ M. D. Simon, L. O. Heflinger and A. K. Geim. Diamagnetically stabilized magnet levitation. American Journal of Physics, 2001.
- ^ Z. Ye, Z. Duan and Y. Su. Theoretical and Numerical Analysis of Diamagnetic Levitation and its Experimental Verification. The International Society for Optics and Photonics, 2014. Y. Li. Magnetic Properties of Solids. Chem268 Solid State and Material Chemistry lecture slide; University of California, 2009.
- ^ I. Vishik. Why is magnetic susceptibility of diamagnetic materials nearly independent of temperature? 2015. https://www.quora.com/Why-is-magnetic¬susceptibility-of-diamagnetic-materials-nearly-independent-of¬temperature
- ^ N. Olsen, N. Lühr, T. J. Sabaka, M. Mandea, M. Rother, L. Tøffner-Clausen and S. Choi. CHAOS—a model of the Earth’s magnetic field derived from CHAMP, Ørsted, and SAC-C magnetic satellite data. Geophysics Journal International, 2006.
- ^ C. C. Finlay, N. Olsen and L. Tøffner-Clausen. DTU candidate field models for IGRF¬12 and the CHAOS-5 geomagnetic field model. DTU Space, Technical University of Denmark, 2014.
- ^ H. Yaghoubi, N. Barazi and M. Aoliaei. Maglev, Infrastructure Design, Signaling and Security in Railway. InTech, 2012.